La derivada es uno de los conceptos más importante en matemáticas. La derivada es el resultado de un límite y representa la pendiente de la recta tangente a la gráfica de la función en un punto. Pero vayamos por partes.
La definición de derivada es la siguiente:
propiedades:
- Derivada de la suma: es la suma de las derivadas
- Derivada del producto por una constante c
- Derivada del producto de funciones
- Si g no se anula, entonces, la derivada del cociente es
- Regla de la cadena
ejercicios:
1.-hallar la derivada de :
Como la función es una suma, su derivada es la suma de las derivadas. La derivada de cada sumando es la derivada de un cociente:
Para facilitar la escritura, calculamos las derivadas por separado: sean las funciones
Las derivadas son:
Luego la derivada de la función es:
2.-hallar la derivada de:
Se trata de un cociente. Notemos que la exponencial tiene la variable al cuadrado y dentro del logaritmo tenemos un coseno elevado a 5.
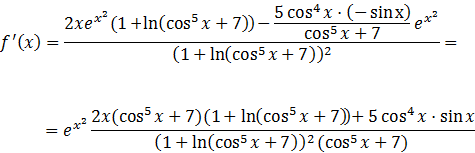
3.-halla la derivada de:
solución:
4.- halla la derivada de :
solucion:
Tenemos de nuevo una exponencial con base distinta de e.
Problemas:
Se quiere construir una caja sin tapa a partir de una hoja de cartón de 20x10cm. Para ello, se corta un cuadrado de lado L en cada esquina y se dobla la hoja levantando los cuatro laterales de la caja.
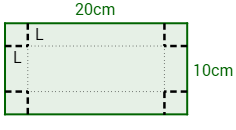
Determinar las dimensiones de la caja para que su volumen sea máximo si el lado (L) debe medir entre 2 y 3 cm
Si (a) es el ancho de la caja,(h) es su altura y (p) es su profundidad, entonces su volumen es
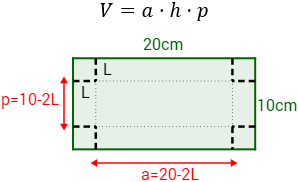
Al cortar los cuatro cuadrados de lado (L), el ancho de la caja es
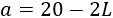
La profundidad es
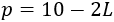
Por último, la altura coincide con el lado del cuadrado recortado:
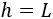
Luego el volumen de la caja en función de (L) es (paso 1)
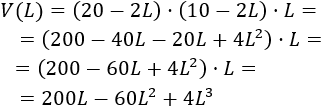
Derivamos la función volumen (paso 2):
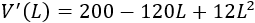
Igualamos a 0 la derivada y resolvemos la ecuación para encontrar los puntos críticos (paso 3):
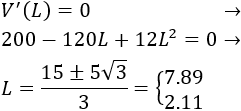
Situamos los puntos en la recta real y estudiamos los signos en los intervalos (paso 4):

Escogemos los puntos (x=1) del primer intervalo, (x =3) del segundo intervalo y (x=8) del tercero:
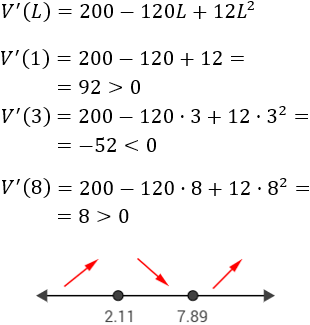
Luego la función es creciente en el primer intervalo, decreciente en el segundo y creciente en el tercero:
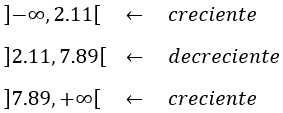
Pero el lado (L) debe medir entre 2 y 3, es decir, debe ser
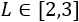
Como en el intervalo ([2.11, 3]) la función es decreciente, el volumen será máximo para (L=2.11cm).
Por tanto, las dimensiones de la caja deben ser

Es decir, las dimensiones son 15.78 x 5.78 x 2.11 cm y su volumen es (192.45 cm2).
2.-Una empresa vende 0.7 toneladas de zumo y 0.3 toneladas de sobrante por cada tonelada de materia prima. El coste de la materia prima es de 0.8€/kg, los precios de venta del zumo y del sobrante son 2.5€/kg y 0.05€/kg, respectivamente, y el coste de producción viene dado por la función
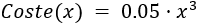
donde (x) representa las toneladas de zumo producido.
Obtener:
- Una expresión para calcular las ganancias netas en función de las toneladas de materia prima.
- La cantidad de zumo que se debe fabricar para que las ganancias netas sean máximas.
Sea (x) la cantidad de materia prima y sean (z) y (s) las cantidades de zumo y de sobrante, respectivamente.
El número de toneladas de zumo producido en función de las toneladas de materia prima es
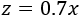
Y el de sobrante,
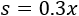
Las ganancias brutas son:
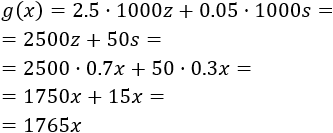
Hemos multiplicado por 1000 porque el precio es por kilo y no por tonelada.
El coste total es el coste de la materia prima más el coste de producción:
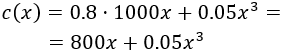
Luego las ganancias netas en función de las toneladas de materia prima son:
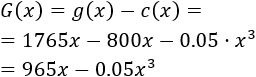
Calculamos la derivada:
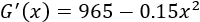
Igualamos la derivada a 0 y resolvemos la ecuación para buscar puntos críticos:
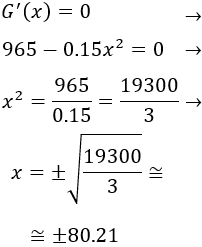
Representamos los puntos obtenidos en la recta real y estudiamos el signo de la derivada:

Elegimos el punto (x=-100) del primer intervalo, el punto (x = 0) del segundo y el punto (x =100) del tercer intervalo:

Por el criterio de la primera derivada, la función es decreciente en el primer y tercer intervalo y creciente en el segundo:
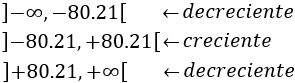
Nota: podemos acotar el dominio de la función al intervalo de los reales positivos ya que no tiene sentido que se produzcan cantidades negativas de zumo.
De la monotonía, deducimos que en el punto (x=-80.21) la función tiene un mínimo y en el punto (x = 80.21) tiene un máximo.
Por tanto, las ganancias netas son máximas cuando la cantidad de materia prima es 80.21 toneladas. En toneladas de zumo, equivale a 56.15 toneladas ya que
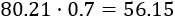
APLICACIONES A LA GEOMETRÍA:
- La derivada de la superficie o área es la longitud.
- La derivada del volumen es la superficie.
APLICACIONES A LA FÍSICA:
CINEMÁTICA
- La velocidad instantánea es la derivada del espacio respecto del tiempo.
- La aceleración instantánea es la derivada de la velocidad respecto del tiempo. Por tanto, la aceleración instantánea es la segunda derivada del espacio respecto del tiempo.
DINÁMICA
- La derivada del momento lineal con el tiempo es la fuerza.
- La derivada de la fuerza con respecto a la posición es la energía (potencial, cinética, trabajo...)
TERMODINÁMICA
- Si una sustancia dada se mantiene a una temperatura constante, entonces su volumen V depende de la presión P. La compresibilidad isotérmica está relacionada con la derivada delvolumen respecto a la presión mediante la siguiente fórmula:
FÍSICA DE MATERIALES
- La derivada de la masa con respecto a la longitud/superficie/volumen es la densidad.
ELECTROSTÁTICA
- La derivada de la carga eléctrica con respecto al tiempo es la intensidad de corriente.
APLICACIONES A LA QUÍMICA:
- Cuando se produce una reacción química, las concentraciones de los reactivos y productos van cambiando con el tiempo hasta que se produce el equilibrio químico, en el cual las concentraciones de todas las sustancias permanecen constantes. La velocidad de reacción química es la derivada de la concentración de un reactivo o producto en función del tiempo.
APLICACIONES A LA BIOLOGÍA:
- Permite el estudio de evolución de poblaciones de bacterias, de otras especies animales, de plantas... Se han deducido expresiones para el "Número de individuos" (tamaño de la población) según el tipo de crecimiento que presentan, y para obtener dicho crecimiento se necesitan las derivadas:
- Se sabe que un material radioactivo se desintegra con una rapidez proporcional a la cantidad presente en cualquier instante, por lo que, usando el cálculo diferencial, se puede encontrar la expresión de la cantidad de material radiactivo en función del tiempo.
APLICACIONES A LA MEDICINA
- El concepto de derivada permite conocer la evolución de ciertas enfermedades puesto que podemos modelizar el número de bacterias, virus, células infectadas... y estudiar su ritmo de crecimiento/decrecimiento al utilizar fármacos, comprobando así su efectividad.
- Podemos estudiar la evolución de ciertas epidemias puesto que podemos modelizar el número de enfermos en función del tiempo transcurrido.
APLICACIONES A LA INGENIERÍA:
- Los ingenieros químicos o ingenieros en procesos utilizan la derivada para representar fenómenos que ocurren en un proceso mediante el uso de ecuaciones diferenciales.
- Se utilizan en los sistemas de tratamiento de aguas residuales así como en la recogida y tratamiento de residuos.
- También son de gran utilidad en los estudios de contaminación y diagnóstico.
- En ingeniería industrial se utiliza mucho la derivada para reducir costes al fabricar un producto (optimización).
APLICACIONES A LA ARQUITECTURA:
- En arquitectura, es frecuente trabajar con curvas complejas (paraboliodes, hiperboloides, superficies irregulares...) de las que necesitamos obtener información relevante (máximos, mínimos, zonas de concavidad y convexidad...)
- También se utiliza la derivada (y la integral) para calcular áreas y volúmenes de regiones y sólidos de revolución.
- Para resolver problemas de optimización (reducir costes de los materiales)
- Resultan de gran utilidad en el diseño de vías y carreteras, más específicamente, en el estudio de su curvatura.
APLICACIONES A LA ECONOMÍA:
- El uso de la derivada permite resolver múltiples problemas de optimización en el ámbito económico (conseguir que una empresa obtenga el máximo beneficio, los ingresos máximos, los costes mínimos...)
- También permite estudiar la evolución de determinados fenómenos de índole económica (índice de la bolsa, evolución de la economía, beneficios de una empresa...) en función del tiempo (crecimiento, decrecimiento, máximos y mínimos...), proporcionando información muy útil para el empresario a la hora de tomar decisiones.
- La derivada es una herramienta de gran utilidad en economía puesto que nos permite realizarcálculos marginales, es decir, hallar la razón de cambio cuando se agrega una unidad adicional al total, sea cual sea la cantidad económica que se esté estudiando (coste, ingreso, beneficio, producción...)



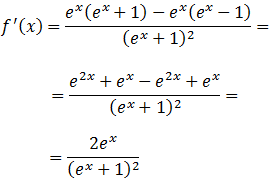

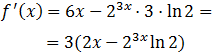












No hay comentarios:
Publicar un comentario