Las funciones exponenciales son las funciones que tienen la variable independiente x en el exponente, es decir, son de la forma:
Las características generales de las funciones exponenciales son:
1) El dominio de una función exponencial es R.
2) Su recorrido es (0, +∞) .
3) Son funciones continuas.
4) Como a0 = 1 , la función siempre pasa por el punto (0, 1).
La función corta el eje Y en el punto (0, 1) y no corta el eje X.
5) Como a1 = a , la función siempre pasa por el punto (1, a).
6) Si a > 1 la función es creciente.
Si 0 < a < 1 la función es decreciente.
7) Son siempre concavas.
8) El eje X es una asíntota horizontal.
- Si a > 1 :
Al elevar un número mayor que 1 a cantidades negativas cada vez más grandes, el valor de la potencia se acerca a cero, por tanto :
Cuando x → - ∞ , entonces a x → 0 - Si 0 < a < 1 :
Ocurre lo contrario que en el caso anterior :
Cuando x → + ∞ , encontes a x → 0
EJEMPLOS:
1.Representa gráficamente y di las propiedades de la función g cuya ecuación es g(x) = 3x+2.
Solución:
Para representar gráficamente esta función:
- Determinas su asíntota horizontal: y = 0.La asíntota horizontal pasa por el valor que está a la derecha de la potencia, en este caso no aparece número alguno.
- Calculas su cero:3x+2 = 0 (Igualas la ecuación a cero)Esta ecuación no tiene solución, ya que una potencia de base positiva nunca es igual a cero.No tiene cero.
- Hallas el intercepto de la gráfica con el eje "y":y = 30+2 (Sustituyes x por cero en la ecuación)y = 32 (Efectúas los cálculos indicados)y = 9
En el sistema de coordenadas trazas la asíntota horizontal, ubicas los puntos hallados y trazas la curva.
2.Sea f una función definida para por la ecuación y = 2x+2 – 8.
b) Analiza sus signos.
c) Determina su valor máximo y su valor mínimo.
d) Indica su monotonía en el intervalo dado.
|
- Solución b)Recuerda que para analizar los signos se toma como referencia el cero de la función, que hallamos anteriormente.La función es:
-
Los valores – 2 y 2 se incluyen en cada intervalo, ya que para esos valores la gráfica está por debajo y por encima, respectivamente, del eje "x".
- Solución c) Determina su valor máximo y su valor mínimo.R/ Las funciones exponenciales no tiene mínimo ni máximo en el caso de estar definida para todos los números reales, pero en este caso como está limitado su dominio.
- Valor mínimo: y = – 7 (Se alcanza en x = – 2)
- Valor máximo: y = 8 (Se alcanza en x = 2)
- Solución d) Indica su monotonía en el intervalo dado.R/ Monótona creciente. (La gráfica asciende de izquierda a derecha)
3.
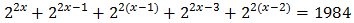
Reescribimos la ecuación
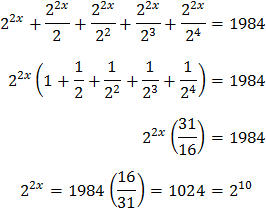 Por tanto, la ecuación exponencial se reduce a una de primer grado:
Por tanto, la ecuación exponencial se reduce a una de primer grado:
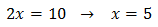
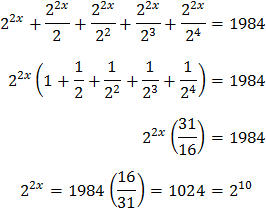
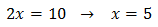
algunos problemas:
1.-En 1966 la Comisión Internacional Contra la Captura de Ballenas protegió a la población mundial de ballena azul contra los barcos balleneros. En 1978 se pensaba que la población en el hemisferio sur era de 5000. Ahora sin depredadores y con abastecimiento abundante de alimentos, se espera que la población crezca exponencialmente de acuerdo con la fórmula
a) Calculamos la población en el año 2000.
b) Pronostica la población en el año 2007.
c) Siguiendo el modelo creado y asumiendo que 0% de natalidad y 1978 como año cero, ¿cuándo se duplicará la cantidad de ballenas azules?
En el año 1993 había el doble de ballenas que en el año 1978.
5.-



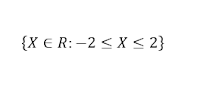






No hay comentarios:
Publicar un comentario