Las funciones matemáticas se utilizan en otros ámbitos, por ejemplo, para calcular los beneficios o los costes de una empresa, la velocidad o aceleración de un móvil, etc., por lo que es importante conocer el comportamiento de una función.
Por ejemplo, la siguiente función no está definida en x=0 ni en x = -1 (porque no se puede dividir entre 0:
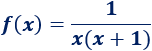
Sin embargo, sí podemos preguntarnos cómo se comporta la función cuando x se aproxima a 0 o cuando se aproxima a -1. ¿Y si x crece o decrece indefinidamente? Los límites de la función f nos proporcionan las respuestas.
Además de ayudarnos a visualizar la gráfica de la función, los límites también se utilizan para estudiar otras propiedades, como la continuidad de una función, la diferenciabilidad, etc.
Ejercicios:
Si sustituimos por obtenemos una indeterminación:
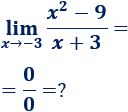
Sin embargo, podemos simplificar la función antes de calcular el límite:
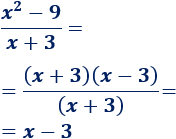
Calculamos el límite (sustituyendo):
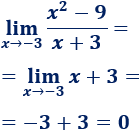
3.-Hallar el límite en el punto x = 1 de la función :
Para este caso, si hallamos el valor de la función en x = 1 obtenemos f(1) = 0/0, que es uno de los casos de indeterminación, lo cual no significa que es imposible hallar el límite de f(x) en ese punto, sino que debemos "operar" para eliminar la indeterminación (por lo general toda indeterminación puede ser determinada). Por ejemplo podemos descomponer en factores el numerador de la fracción:
4.-Hallar el límite en el punto x = 2 de la función y = x² +1 .
Este límite es 5, puesto que de una manera clara tenemos f(2) = 5.
algunos limites trigonométricos, pero antes debemos conocer algunas propiedades:

ahora si, pasemos a los ejercicios:

algunos limites trigonométricos, pero antes debemos conocer algunas propiedades:

ahora si, pasemos a los ejercicios:

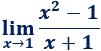
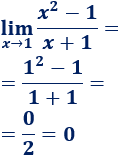
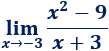


No hay comentarios:
Publicar un comentario