LIMITES AL INFINITO

Una indeterminación matemática es una expresión algebraica que aparece en el cálculo de los límites y cuyo resultado no se puede predecir.
Cuando aparece una indeterminación en un límite, el límite depende de la propia función. Esto conlleva que, aunque aparezca la misma indeterminación, el límite puede ser distinto para funciones distintas.

Las indeterminaciones son las 7 siguientes expresiones:

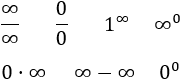
Para las demás expresiones que involucran infinito o partido cero, existen reglas como las siguientes:

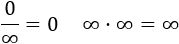
propiedades:

 Cuando se opera con límites de funciones se trabaja con el conjunto R ampliado, es decir, el conjunto de los números reales al que se le han añadido los entes numéricos: +∞, -∞. Conviene, por tanto, tener claras algunas propiedades de estos entes, así como valores que son indeterminados en este conjunto:

  *  Para cualquier número n (incluido el 0):  n/∞= 0.

  *  Para cualquier número n positivo (distinto de 0):  n .+∞= +∞,   n .(-∞)= -∞.

  *  Para cualquier número n negativo (distinto de 0):  n .+∞= -∞,   n .(-∞)= +∞.

  *  Para el caso del 0:    0 . +∞  y   0 . (-∞)  son Indeterminados.  

   *  Para números n positivos +∞/n = +∞, pero para n negativos +∞/n = -∞.

   *  Para el caso del 0:   +∞/0  =  ∞,  así como -∞/0 = ∞,  pero en ambos casos el signo del infinito es Indeterminado .  Algo similar sucede cuando dividimos un número entre cero:  3/0 = ∞, -3/0 = ∞ (el signo del infinito es indeterminado, aunque sí podemos asegurar lo que sucede tanto a la derecha de 0, como a la izquierda de 0 ).

   *  Asimismo son Indeterminados:  

 ∞/∞ (con cualquier signo),  ∞-∞,  0/0 , 0° , ∞° (cualq. signo).

   La mayoría de estas relaciones son muy lógicas si nos acostumbramos a imaginar a  +∞,  como  1/(+0), y a   -∞,  como -1/(+0)  -entendiendo por +0 un número positivo muy pequeño  

ejercicios:

1.-Hallar el siguiente límite en el infinito:

 En principio si sustituimos x por +∞, nos encontramos con la indeterminación ∞-∞, en estos casos suele funcionar multiplicar y dividir por la misma expresión pero con el signo positivo, es decir:

2.- Hallar el siguiente límite en el infinito:

Si sustituimos x por +∞, nos encontramos con la indeterminación ∞/∞. Para estos casos de cocientes de polinomios en el infinito, se sigue la regla: " Dividir numerador y denominador por la potencia máxima del denominador", que en nuestro caso es x³:

3.- Estudiar lo que sucede en x=0 para la función    :

Al tratar de hallar f(0) nos encontramos con el número e elevado al infinito impreciso, por lo tanto pasemos a hallar los límites laterales:

 

   En este caso el límite por la derecha de x=0, es decir para x=0+e ,  nos conduce al número e elevado a 1/e (para esta expresión imagínense, como siempre, algo así como 1/ +0,00000000001), cuyo resultado es e elevado a +∞, o sea, +∞.

 

  En este límite por la izquierda de x=0, es decir para x=0-e ,  nos conduce al número e elevado a -1/e, u

4.-

5.-